6.1. Earthquake Assessment
This example is a small-scale regional earthquake risk assessment which performs response simulation and damage/loss estimation for a group of 20 buildings. The buildings are modeled as elastic-perfectly plastic single-degree-of-freedom (SDOF) systems defined by three input model parameters: the weight W, yield strength f_yield, and fundamental period T1. The buildings are distributed in space in a 4x5 grid, within a 3x3 grid of event sites. At each event site, 5 ground motion records of similar intensity are assigned.
6.1.1. Inputs
The example input files can be downloaded here: example_eq.zip. For more information about required input files, refer to Inputs.
Configuration file: The configuration file specifies all simulation settings, including the application types, input file names, units, and type of outputs.
1{
2 "Name": "rWHALE_",
3 "Author": "Adam Zsarnóczay",
4 "WorkflowType": "Parametric Study",
5 "runDir": "...",
6 "localAppDir": "C:/rWHALE/",
7 "units": {
8 "force": "kips",
9 "length": "in",
10 "time": "sec"
11 },
12 "outputs": {
13 "EDP": true,
14 "DM": true,
15 "DV": true,
16 "every_realization": false
17 },
18 "Applications": {
19 "Building": {
20 "Application": "CSV_to_BIM",
21 "ApplicationData": {
22 "Min": "1",
23 "Max": "2",
24 "buildingSourceFile":"input_params.csv"
25 }
26 },
27 "RegionalMapping": {
28 "Application": "NearestNeighborEvents",
29 "ApplicationData": {
30 "filenameEVENTgrid": "records/EventGrid.csv",
31 "samples": 5,
32 "neighbors": 4
33 }
34 },
35 "Events": [{
36 "EventClassification": "Earthquake",
37 "Application": "SimCenterEvent",
38 "ApplicationData": {
39 "pathEventData": "records/"
40 }
41 }],
42 "Modeling": {
43 "Application": "OpenSeesPyInput",
44 "ApplicationData": {
45 "mainScript": "cantilever.py",
46 "modelPath": "model/",
47 "ndm": 3,
48 "dofMap": "1,2,3"
49 }
50 },
51 "EDP": {
52 "Application": "UserDefinedEDP_R",
53 "ApplicationData": {
54 "EDPspecs": "EDP_specs.json"
55 }
56 },
57 "Simulation": {
58 "Application": "OpenSeesPy-Simulation",
59 "ApplicationData": {
60 }
61 },
62 "UQ": {
63 "Application": "Dakota-UQ",
64 "ApplicationData": {
65 "method": "LHS",
66 "samples": 5,
67 "type": "UQ",
68 "concurrency": 1,
69 "keepSamples": true
70 }
71 },
72 "DL": {
73 "Application": "pelicun",
74 "ApplicationData": {
75 "DL_Method": "HAZUS MH EQ",
76 "Realizations": 5,
77 "detailed_results": false,
78 "log_file": true,
79 "coupled_EDP": true,
80 "event_time": "off",
81 "ground_failure": false
82 }
83 }
84 }
85}
Building Application: This example uses the CSV_to_BIM building application. In the configuration file, the Max and Min parameters are set to run the full set of 20 buildings, and the name of the building source file is provided as “input_params.csv”. In the building source file, input parameters for (a) the response simulation (weight
W, yield strengthf_yield, and fundamental periodT1) and for (b) the DL assessment (e.g.,NumberofStories,YearBuilt,OccupancyClass,StructureType,PlanArea,ReplacementCost) are specified.
Building source file:
id |
Latitude |
Longitude |
NumberofStories |
YearBuilt |
OccupancyClass |
StructureType |
PlanArea |
ReplacementCost |
W |
f_yield |
T1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
0 |
37.422 |
-122.182 |
1 |
1957 |
RES1 |
W1 |
1293.253476 |
1 |
55.25 |
118.75 |
0.29375 |
1 |
37.422 |
-122.18575 |
1 |
1927 |
RES1 |
W1 |
2568.835761 |
1 |
86.75 |
148.75 |
0.15625 |
2 |
37.422 |
-122.1895 |
1 |
2020 |
RES1 |
W1 |
1127.07738 |
1 |
114.75 |
123.75 |
0.39375 |
3 |
37.422 |
-122.19325 |
1 |
1951 |
RES1 |
W1 |
2085.809768 |
1 |
107.75 |
126.25 |
0.24375 |
4 |
37.422 |
-122.197 |
1 |
1960 |
RES1 |
W1 |
1481.567067 |
1 |
76.25 |
101.25 |
0.30625 |
5 |
37.42366667 |
-122.182 |
1 |
1986 |
RES1 |
W1 |
1240.719532 |
1 |
90.25 |
116.25 |
0.21875 |
6 |
37.42366667 |
-122.18575 |
1 |
1984 |
RES1 |
W1 |
2437.970509 |
1 |
93.75 |
141.25 |
0.35625 |
7 |
37.42366667 |
-122.1895 |
1 |
1983 |
RES1 |
W1 |
2668.60615 |
1 |
111.25 |
133.75 |
0.36875 |
8 |
37.42366667 |
-122.19325 |
1 |
1957 |
RES1 |
W1 |
1553.47035 |
1 |
104.25 |
108.75 |
0.19375 |
9 |
37.42366667 |
-122.197 |
1 |
1984 |
RES1 |
W1 |
1625.164708 |
1 |
58.75 |
106.25 |
0.23125 |
10 |
37.42533333 |
-122.182 |
1 |
2018 |
RES1 |
W1 |
1787.865419 |
1 |
62.25 |
143.75 |
0.34375 |
11 |
37.42533333 |
-122.18575 |
1 |
2018 |
RES1 |
W1 |
1821.174819 |
1 |
65.75 |
138.75 |
0.20625 |
12 |
37.42533333 |
-122.1895 |
1 |
1930 |
RES1 |
W1 |
1624.532488 |
1 |
69.25 |
146.25 |
0.31875 |
13 |
37.42533333 |
-122.19325 |
1 |
1922 |
RES1 |
W1 |
1134.673241 |
1 |
79.75 |
103.75 |
0.25625 |
14 |
37.42533333 |
-122.197 |
1 |
1947 |
RES1 |
W1 |
1625.097354 |
1 |
51.75 |
128.75 |
0.16875 |
15 |
37.427 |
-122.182 |
1 |
1969 |
RES1 |
W1 |
2289.96328 |
1 |
83.25 |
131.25 |
0.33125 |
16 |
37.427 |
-122.18575 |
1 |
2006 |
RES1 |
W1 |
2288.360712 |
1 |
100.75 |
136.25 |
0.38125 |
17 |
37.427 |
-122.1895 |
1 |
1959 |
RES1 |
W1 |
2291.605647 |
1 |
97.25 |
111.25 |
0.18125 |
18 |
37.427 |
-122.19325 |
1 |
1979 |
RES1 |
W1 |
2770.811412 |
1 |
72.75 |
113.75 |
0.26875 |
19 |
37.427 |
-122.197 |
1 |
1976 |
RES1 |
W1 |
2088.450773 |
1 |
118.25 |
121.25 |
0.28125 |
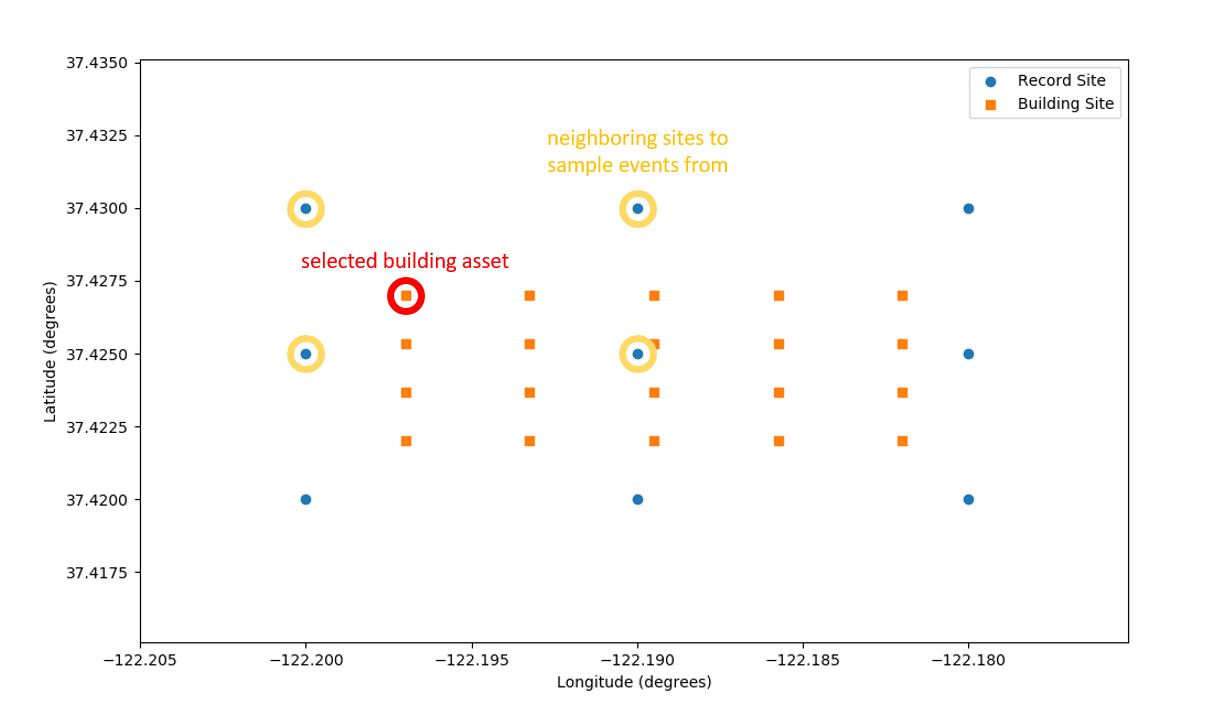
Regional Mapping Application: This example uses the NearestNeighborEvents regional mapping application. From the parameters set in the configuration file, the algorithm is set to randomly select 5 samples of ground motion records from the 4 nearest neighbors for each building asset.
Event Application: This example uses the SimCenterEvents event application. It takes as input the EventGrid.csv, event files with the ground motion intensity measures, and the site files which specify the five ground motions assigned to each event site.
Event grid file:
sta |
lon |
lat |
|---|---|---|
site0.csv |
-122.18 |
37.42 |
site1.csv |
-122.19 |
37.42 |
site2.csv |
-122.2 |
37.42 |
site3.csv |
-122.18 |
37.425 |
site4.csv |
-122.19 |
37.425 |
site5.csv |
-122.2 |
37.425 |
site6.csv |
-122.18 |
37.43 |
site7.csv |
-122.19 |
37.43 |
site8.csv |
-122.2 |
37.43 |
Site file:
GM_file |
factor |
|---|---|
RSN251 |
4.683735054680426 |
RSN564 |
1.2243750794265975 |
RSN692 |
0.8188602253372889 |
RSN626 |
1.252450834874058 |
RSN244 |
4.634837258912294 |
Modeling Application: This example uses the OpenSeesPyInput modeling application. The buildings are modeled as elastic-perfectly plastic single-degree-of-freedom (SDOF) systems defined by three input model parameters: the weight
W, yield strengthf_yield, and fundamental periodT1. Functions are included which record the peak response as EDPs for each of the EDP types specified in the EDP_specs.json file.
Model file:
1import numpy as np
2from math import pi, sqrt
3from openseespy.opensees import *
4import os
5
6
7''' FUNCTION: build_model ------------------------------------------------------
8Generates OpenSeesPy model of an elastic-perfectly plastic SDOF system and runs
9gravity analysis.
10Inputs: in model_params
11 W - weight of structure
12 f_yield - yield stiffness
13 T1 - fundamental period
14Outputs:
15
16-----------------------------------------------------------------------------'''
17
18def build_model(model_params):
19
20 G = 386.1
21 W = model_params["W"]
22 f_yield = model_params["f_yield"]
23 T1 = model_params["T1"]
24 m = W / G
25 print("m: " + str(m))
26
27 # set model dimensions and deg of freedom
28 model('basic', '-ndm', 3, '-ndf', 6)
29
30 # define nodes
31 base_node_tag = 10000
32 top_node_tag = 10001
33 height = 240. # in
34 node(base_node_tag, 0., 0., 0.)
35 node(top_node_tag, 0., 0., height)
36
37 # define fixities
38 fix(base_node_tag, 1, 1, 1, 1, 1, 1)
39 fix(top_node_tag, 0, 0, 0, 1, 1, 1)
40
41 # define bilinear (elastic-perfectly plastic) material
42 material_tag = 100
43 stiffmat = 110
44 K = m / (T1/(2*pi))**2
45 print("K: " + str(K))
46 uniaxialMaterial('Steel01', material_tag, f_yield, K, 0.0001)
47 uniaxialMaterial('Elastic', stiffmat, 1.e9)
48
49 # define element
50 element_tag = 1000
51 element('twoNodeLink', element_tag, base_node_tag, top_node_tag, '-mat', stiffmat, material_tag, material_tag, '-dir', 1, 2, 3, '-orient', 0., 0., 1., 0., 1., 0., '-doRayleigh')
52
53 # define mass
54 mass(top_node_tag, m, m, m, 0., 0., 0.)
55
56 # define gravity loads
57 # W = m * 386.01 # g
58 timeSeries('Linear', 1)
59 pattern('Plain', 101, 1)
60 load(top_node_tag, 0., 0., -W, 0., 0., 0.)
61
62 # define damping based on first eigenmode
63 damp_ratio = 0.05
64 angular_freq = eigen(1)[0]**0.5
65 beta_k = 2 * damp_ratio / angular_freq
66 rayleigh(0., beta_k, 0., 0.)
67
68 # run gravity analysis
69 tol = 1e-8 # convergence tolerance for test
70 iter = 100 # max number of iterations
71 nstep = 100 # apply gravity loads in 10 steps
72 incr = 1./nstep # first load increment
73
74 # analysis settings
75 constraints('Transformation') # enforce boundary conditions using transformation constraint handler
76 numberer('RCM') # renumbers dof's to minimize band-width (optimization)
77 system('BandGeneral') # stores system of equations as 1D array of size bandwidth x number of unknowns
78 test('EnergyIncr', tol, iter, 0) # tests for convergence using dot product of solution vector and norm of right-hand side of matrix equation
79 algorithm('Newton') # use Newton's solution algorithm: updates tangent stiffness at every iteration
80 integrator('LoadControl', incr) # determine the next time step for an analysis # apply gravity in 10 steps
81 analysis('Static') # define type of analysis, static or transient
82 analyze(nstep) # perform gravity analysis
83
84 # after gravity analysis, change time and tolerance for the dynamic analysis
85 loadConst('-time', 0.0)
86
87
88
89
90
91
92# FUNCTION: PeakDriftRecorder --------------------------------------------------
93# saves envelope of interstory drift ratio for each story at one analysis step
94# ------------------------------------------------------------------------------
95
96def PeakDriftRecorder(EDP_specs, envDict):
97 # inputs:
98 # EDP_specs = dictionary of EDP type, location, direction
99 # envDict = dictionary of envelope values
100
101
102 for loc in EDP_specs['PID']:
103 pos = 0
104 for dof in EDP_specs['PID'][loc]:
105 storynodes = [int(x) for x in EDP_specs['PID'][loc][dof]]
106 # print("computing drifts for nodes: {}".format(storynodes))
107 story_height = nodeCoord(storynodes[1],3) - nodeCoord(storynodes[0],3)
108 # compute drift
109 topDisp = nodeDisp(storynodes[1],dof)
110 botDisp = nodeDisp(storynodes[0],dof)
111 new_drift = abs((topDisp-botDisp)/story_height)
112 # update dictionary
113 curr_drift = envDict['PID'][loc][pos]
114 new_max = max(new_drift, curr_drift)
115 envDict['PID'][loc][pos] = new_max
116 pos += 1
117
118 return envDict
119
120
121
122# FUNCTION: AccelHistoryRecorder -----------------------------------------------
123# saves time history of relative floor acceleration for each story at one analysis step
124# ------------------------------------------------------------------------------
125
126def AccelHistoryRecorder(EDP_specs, histDict, count):
127 # inputs:
128 # histDict = dictionary of time histories
129 # recorderNodes = list of nodes where EDP is recorded
130 # count = current count in the time history
131
132 for loc in EDP_specs['PFA']:
133 for dof in EDP_specs['PFA'][loc]:
134 storynode = int(EDP_specs['PFA'][loc][dof][0])
135 # obtain acceleration
136 new_acc = nodeAccel(storynode, dof)
137 histDict['accel'][loc][dof][count] = new_acc
138
139
140 return histDict
141
142
143
144# FUNCTION: RunDynamicAnalysis -------------------------------------------------
145# performs dynamic analysis and records EDPs in dictionary
146# ------------------------------------------------------------------------------
147
148def RunDynamicAnalysis(tol,iter,dt,driftLimit,EDP_specs,subSteps,GMX,GMZ):
149 # inputs:
150 # tol = tolerance criteria to check for convergence
151 # iter = max number of iterations to check
152 # dt = time increment for analysis
153 # driftLimit = percent interstory drift limit indicating collapse
154 # recorderNodes = vector of node labels used to check global drifts and record EDPs
155 # subSteps = number of subdivisions in cases of ill convergence
156 # GMX = list of GM acceleration ordinates in X direction
157 # GMZ = list of GM acceleration ordinates in Z direction
158
159 # pad shorter record with zeros (free vibration) such that two horizontal records are the same length
160 nsteps = max(len(GMX),len(GMZ))
161 if len(GMX) < nsteps:
162 diff = nsteps - len(GMX)
163 GMX.extend(np.zeros(diff))
164 if len(GMZ) < nsteps:
165 diff = nsteps - len(GMZ)
166 GMZ.extend(np.zeros(diff))
167
168
169 # generate time array from recording
170 time_record = np.linspace(0,nsteps*dt,num=nsteps,endpoint=False)
171
172 # initialize dictionary of envelope EDPs
173 envelopeDict = {}
174 for edp in EDP_specs:
175 envelopeDict[edp] = {}
176 for loc in EDP_specs[edp]:
177 numdof = len(EDP_specs[edp][loc])
178 envelopeDict[edp][loc] = np.zeros(numdof).tolist()
179
180 print(envelopeDict)
181
182 # initialize dictionary of time history EDPs
183 historyDict = {'accel':{}}
184 time_analysis = np.zeros(nsteps*5)
185 for loc in EDP_specs['PFA']:
186 historyDict['accel'][loc] = {}
187 for dof in EDP_specs['PFA'][loc]:
188 historyDict['accel'][loc][dof] = np.zeros(nsteps*5)
189
190 # number of diaphragm levels
191 levels = len(EDP_specs['PFA'])
192 CODnodes = []
193 for loc in EDP_specs['PFA']:
194 CODnodes.append(int(EDP_specs['PFA'][loc][1][0]))
195
196 print(CODnodes)
197
198
199 constraints('Transformation') # handles boundary conditions based on transformation equation method
200 numberer('RCM') # renumber dof's to minimize band-width (optimization)
201 system('UmfPack') # constructs sparse system of equations using UmfPack solver
202 test('NormDispIncr',tol,iter) # tests for convergence using norm of left-hand side of matrix equation
203 algorithm('NewtonLineSearch') # use Newton's solution algorithm: updates tangent stiffness at every iteration
204 integrator('Newmark', 0.5, 0.25) # Newmark average acceleration method for numerical integration
205 analysis('Transient') # define type of analysis: time-dependent
206
207 # initialize variables
208 maxDiv = 1024
209 minDiv = subSteps
210 step = 0
211 ok = 0
212 breaker = 0
213 maxDrift = 0
214 count = 0
215
216 while step<nsteps and ok==0 and breaker==0:
217 step = step + 1 # take 1 step
218 ok = 2
219 div = minDiv
220 length = maxDiv
221 while div<=maxDiv and length>0 and breaker==0:
222 stepSize = dt/div
223 ok = analyze(1,stepSize) # perform analysis for one increment; will return 0 if no convergence issues
224 if ok==0:
225 count = count + 1
226 length = length - maxDiv/div
227 # check if drift limits are satisfied
228 level = 1
229 while level < levels:
230 story_height = nodeCoord(CODnodes[level],3)-nodeCoord(CODnodes[level-1],3)
231 # check X direction drifts (direction 1)
232 topDisp = nodeDisp(CODnodes[level],1)
233 botDisp = nodeDisp(CODnodes[level-1],1)
234 deltaDisp = abs(topDisp-botDisp)
235 drift = deltaDisp/story_height
236 if drift >= driftLimit:
237 breaker = 1
238 # check Y direction drifts (direction 2)
239 topDisp = nodeDisp(CODnodes[level],2)
240 botDisp = nodeDisp(CODnodes[level-1],2)
241 deltaDisp = abs(topDisp-botDisp)
242 drift = deltaDisp/story_height
243 if drift >= driftLimit:
244 breaker = 1
245 # move on to check next level
246 level = level + 1
247 # save parameter values in recording dictionaries at every step
248 time_analysis[count] = time_analysis[count-1]+stepSize
249 envelopeDict = PeakDriftRecorder(EDP_specs, envelopeDict)
250 historyDict = AccelHistoryRecorder(EDP_specs, historyDict, count)
251 else: # if ok != 0
252 div = div*2
253 print("Number of increments increased to ",str(div))
254 # end analysis once drift limit has been reached
255 if breaker == 1:
256 ok = 1
257 print("Collapse drift has been reached")
258
259 print("Number of analysis steps completed: {}".format(count))
260
261 # remove extra zeros from time history
262 time_analysis = time_analysis[1:count+1]
263 historyDict['time'] = time_analysis.tolist()
264
265 # remove extra zeros from accel time history, add GM to obtain absolute acceleration, and record envelope value
266 GMX_interp = np.interp(time_analysis, time_record, GMX)
267 GMZ_interp = np.interp(time_analysis, time_record, GMZ)
268 for level in range(0,levels):
269 # X direction
270 historyDict['accel'][level][1] = historyDict['accel'][level][1][1:count+1]
271 historyDict['accel'][level][1] = np.asarray(historyDict['accel'][level][1]) + GMX_interp
272 envelopeDict['PFA'][level][0] = max(abs(historyDict['accel'][level][1]))
273 # Z direction
274 historyDict['accel'][level][2] = historyDict['accel'][level][2][1:count+1]
275 historyDict['accel'][level][2] = np.asarray(historyDict['accel'][level][2]) + GMZ_interp
276 envelopeDict['PFA'][level][1] = max(abs(historyDict['accel'][level][2]))
277
278
279 return envelopeDict
280
281
282
283# MAIN: run_analysis -----------------------------------------------------------
284# runs dynamic analysis for single event and returns dictionary of envelope EDPs
285# ------------------------------------------------------------------------------
286
287def run_analysis(GM_dt, GM_npts, TS_List, EDP_specs):
288 # inputs:
289 # GM_dt = time step of GM record
290 # GM_npts = number of steps in GM record
291 # TS_List = 1x2 list where first component is a list of GMX acceleration points, second component is a list of GMZ acceleration points (scaled and multipled by G)
292 GMX_points = TS_List[0]
293 GMZ_points = TS_List[1]
294
295 # print(EDP_specs)
296
297 wipeAnalysis()
298
299
300 # define parameters for dynamic analysis
301 driftLimit = 0.20 # %
302 toler = 1.e-08
303 maxiter = 30
304 subSteps = 2
305
306 envdata = RunDynamicAnalysis(toler,maxiter,GM_dt,driftLimit,EDP_specs,subSteps,GMX_points,GMZ_points)
307 print(envdata)
308
309 return envdata
EDP Application: This example uses the UserDefinedEDP EDP application. Custom EDPs are specified in the EDP specifications file. The EDP types are peak interstory drift (PID) and peak floor acceleration (PFA), recorded at the base and top node of the structural model in two horizontal directions (1,2).
EDP specifications file:
1{
2 "locations": {
3 "0": [
4 10000,
5 10001
6 ]
7 },
8 "EDP_types": {
9 "PID": {
10 "0": [
11 1,
12 2
13 ]
14 },
15 "PFA": {
16 "0": [
17 1,
18 2
19 ]
20 }
21 }
22}
Simulation Application: This example uses the OpenSeesPySimulation simulation application, which corresponds to the OpenSeesPyInput modeling application. It reads the
build_modelandrun_analysisfunctions from the model file to perform the response simulation.UQ Application: This example uses the Dakota-UQ UQ application to run the response simulation. In the configuration file, the number of samples specified for the UQ application should match the number of ground motion samples per building asset specified for the RegionalMapping application.
DL Application: This example uses the pelicun DL application. From the building source file, since the DL method selected is “HAZUS MH EQ”, damage/loss estimation is performed using the HAZUS loss assessment method based on earthquake EDPs produced from the response simulation.
6.1.2. Run Workflow
The workflow can be executed by uploading the appropriate files to DesignSafe, or by running the example on your local desktop, using the following initialization command in the terminal:
python "C:/rWHALE/applications/Workflow/R2D_workflow.py" "C:/rWHALE/cantilever_example/rWHALE_config_eq.json" --registry "C:/rWHALE/applications/Workflow/WorkflowApplications.json" --referenceDir "C:/rWHALE/cantilever_example/input_data/" -w "C:/rWHALE/cantilever_example/results"
This command locates the backend applications in the folder “applications”, and the input files in a directory “cantilever_example”. Please ensure that the paths in the command appropriately identify the locations of the files in your directory.
applications
cantilever_example
├── rWHALE_config_eq.json # configuration file
└── input_data
├── model
├── cantilever.py # model file
├── records
├── EventGrid.csv # event grid file
├── RSN30.json # event IM files
├── RSN63.json
.
.
.
├── site0.csv # site files
├── site1.csv
.
.
.
└── site8.csv
├── EDPspecs.json # EDP specifications file
└── input_params.csv # building source file
6.1.3. Outputs
The example output files can be downloaded here: output_data_eq.zip. For more information about the output files produced, refer to Outputs.
EDP_1-19.csv: reports statistics on the EDP results from simulating 5 ground motions for each building asset. The statistics reported are the median and lognormal standard deviation of peak interstory drift (PID) and peak floor acceleration (PFA) in two directions.
type |
PFA |
PFA |
PFA |
PFA |
PFA |
PFA |
PFA |
PFA |
PID |
PID |
PID |
PID |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
loc |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
dir |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
stat |
median |
beta |
median |
beta |
median |
beta |
median |
beta |
median |
beta |
median |
beta |
1 |
141.097 |
0.199749331936861 |
136.972 |
0.26159704860592325 |
412.267 |
0.3689067092818622 |
271.872 |
0.4675055669073214 |
0.00105633 |
0.4186167860756997 |
0.0006980389999999999 |
0.5784022941837268 |
2 |
131.247 |
0.4175448180418805 |
155.204 |
0.20283668507914568 |
176.59 |
0.4337498687956456 |
157.04 |
0.2691536257751124 |
0.00287297 |
0.4355512490436657 |
0.00255504 |
0.2712436832366108 |
3 |
144.195 |
0.3556909851130682 |
138.769 |
0.14200186407081142 |
446.805 |
0.37406788320556 |
317.6 |
0.232094515864188 |
0.00278474 |
0.42430956257276864 |
0.00198152 |
0.3651330947055237 |
4 |
141.43 |
0.2621121131463965 |
149.726 |
0.13936603018873167 |
252.456 |
0.20223535336029075 |
358.745 |
0.4682999285137096 |
0.00248399 |
0.20078394541079414 |
0.00353105 |
0.4664649292002271 |
5 |
127.76799999999999 |
0.1933699100399082 |
162.64700000000005 |
0.22228311460245634 |
373.093 |
0.2695036478790295 |
361.592 |
0.21513981161420967 |
0.0018780000000000001 |
0.2699071050235337 |
0.00181748 |
0.2155059270390112 |
6 |
182.01400000000004 |
0.1878891925155105 |
160.911 |
0.19737203237767328 |
292.335 |
0.48771266468706703 |
292.813 |
0.2930718377890685 |
0.00389908 |
0.4877100061602449 |
0.00390263 |
0.2931719410768729 |
7 |
130.996 |
0.3926228335954007 |
145.494 |
0.09229922720084753 |
267.488 |
0.237269603979 |
146.707 |
0.3405650974061709 |
0.00382051 |
0.2371602524305522 |
0.00209569 |
0.3414405710280442 |
8 |
130.996 |
0.3926228335954007 |
145.494 |
0.09229922720084753 |
416.75300000000004 |
0.12180918060252133 |
417.148 |
0.07443597424038638 |
0.00205192 |
0.3104238725586141 |
0.00182858 |
0.13467088219923146 |
9 |
143.016 |
0.24358377366199915 |
163.14200000000002 |
0.2019342858851748 |
405.908 |
0.35204871925623343 |
322.71 |
0.08340885973141009 |
0.00227816 |
0.3537066848027953 |
0.00181325 |
0.083987554229959 |
10 |
183.49 |
0.18755333115184367 |
160.376 |
0.13276066086178542 |
488.46 |
0.23272021112520425 |
346.295 |
0.38094421218731933 |
0.00606391 |
0.2332570737380188 |
0.00429183 |
0.3818933891243802 |
11 |
146.18 |
0.18278485835299355 |
160.911 |
0.1991058705931532 |
331.755 |
0.2799965748805636 |
484.579 |
0.32562150845640137 |
0.0014824999999999999 |
0.2803097978527769 |
0.0021631 |
0.3249379345839239 |
12 |
130.996 |
0.3926228335954007 |
145.494 |
0.09229922720084753 |
254.428 |
0.28072218931094045 |
288.997 |
0.3930704970844931 |
0.00271677 |
0.2812514879339413 |
0.0030816 |
0.3928937764199453 |
13 |
143.016 |
0.3786819120652951 |
175.497 |
0.12506807756500646 |
289.259 |
0.12209314196371647 |
311.926 |
0.2268268415312083 |
0.00199303 |
0.12220673894617105 |
0.00215043 |
0.2271012433659633 |
14 |
143.016 |
0.3895371771421967 |
131.827 |
0.2150120977551468 |
425.28600000000006 |
0.18182010821614525 |
473.92900000000003 |
0.1144372496639498 |
0.0012720000000000001 |
0.1819342336642664 |
0.00141906 |
0.11431467535648035 |
15 |
182.01400000000004 |
0.3608990379206519 |
147.194 |
0.2253981063223195 |
389.17800000000005 |
0.3543220031783357 |
428.847 |
0.3687617252701749 |
0.00448564 |
0.3545767941681689 |
0.00494268 |
0.3692013703541936 |
16 |
157.774 |
0.3836750491797111 |
130.084 |
0.19764143187735794 |
287.992 |
0.5030060338225658 |
378.276 |
0.4394897070740103 |
0.00439757 |
0.5081468202869077 |
0.005776399999999999 |
0.43938961960039613 |
17 |
131.71 |
0.3920062442871513 |
150.631 |
0.09242281539618902 |
455.541 |
0.13776975495264546 |
454.36 |
0.2490103895868422 |
0.00176016 |
0.2861092987848653 |
0.00161805 |
0.26566745390451 |
18 |
143.016 |
0.4079243417920144 |
160.911 |
0.14065793137491145 |
297.425 |
0.22852660788272866 |
307.39 |
0.25192434465967034 |
0.00225423 |
0.2287664511405949 |
0.00233144 |
0.2520961518809855 |
19 |
137.914 |
0.4224669047258293 |
131.827 |
0.2054938432485909 |
249.41099999999997 |
0.2679721569521585 |
409.027 |
0.2668373210824858 |
0.0020721 |
0.28311021269960546 |
0.00360748 |
0.31569408537266186 |
DM_1-19.csv: reports collapse probability and damage state probability for each building asset.
Collapse |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
DS likelihood |
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
comp_type |
probability |
S |
S |
S |
S |
S |
S |
NS |
NS |
NS |
NS |
NS |
NSA |
NSA |
NSA |
NSA |
NSA |
NSD |
NSD |
NSD |
NSD |
NSD |
DSG_DS |
0 |
1_1 |
2_1 |
3_1 |
4_1 |
4_2 |
0 |
1_1 |
2_1 |
3_1 |
4_1 |
0 |
1_1 |
2_1 |
3_1 |
4_1 |
0 |
1_1 |
2_1 |
3_1 |
4_1 |
|
1 |
0.0 |
1.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.4 |
0.2 |
0.2 |
0.2 |
0.0 |
0.4 |
0.2 |
0.2 |
0.2 |
1.0 |
0.0 |
0.0 |
0.0 |
0.0 |
2 |
0.0 |
0.6 |
0.4 |
0.0 |
0.0 |
0.0 |
0.0 |
0.2 |
0.20000000000000007 |
0.4 |
0.0 |
0.2 |
0.2 |
0.20000000000000007 |
0.4 |
0.0 |
0.2 |
0.8 |
0.2 |
0.0 |
0.0 |
0.0 |
3 |
0.0 |
0.4 |
0.6 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.2 |
0.4 |
0.0 |
0.4 |
0.0 |
0.2 |
0.4 |
0.0 |
0.4 |
0.6 |
0.4 |
0.0 |
0.0 |
0.0 |
4 |
0.0 |
0.4 |
0.6 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.4 |
0.2 |
0.2 |
0.2 |
0.0 |
0.4 |
0.2 |
0.2 |
0.2 |
0.4 |
0.4 |
0.2 |
0.0 |
0.0 |
5 |
0.0 |
1.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.4 |
0.0 |
0.4 |
0.2 |
0.0 |
0.4 |
0.0 |
0.4 |
0.2 |
0.8 |
0.2 |
0.0 |
0.0 |
0.0 |
6 |
0.0 |
0.4 |
0.6 |
0.0 |
0.0 |
0.0 |
0.0 |
0.2 |
0.20000000000000007 |
0.6 |
0.0 |
0.0 |
0.2 |
0.20000000000000007 |
0.6 |
0.0 |
0.0 |
0.6 |
0.2 |
0.2 |
0.0 |
0.0 |
7 |
0.0 |
0.4 |
0.6 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.4 |
0.2 |
0.4 |
0.0 |
0.0 |
0.4 |
0.2 |
0.4 |
0.0 |
0.2 |
0.8 |
0.0 |
0.0 |
0.0 |
8 |
0.0 |
1.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.2 |
0.6000000000000001 |
0.2 |
0.0 |
0.0 |
0.2 |
0.6000000000000001 |
0.2 |
0.8 |
0.2 |
0.0 |
0.0 |
0.0 |
9 |
0.0 |
0.8 |
0.2 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.2 |
0.8 |
0.0 |
0.0 |
0.0 |
0.2 |
0.8 |
0.0 |
0.0 |
0.4 |
0.6 |
0.0 |
0.0 |
0.0 |
10 |
0.0 |
0.6 |
0.4 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.4 |
0.2 |
0.4 |
0.0 |
0.0 |
0.4 |
0.2 |
0.4 |
0.6 |
0.2 |
0.2 |
0.0 |
0.0 |
11 |
0.0 |
1.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.2 |
0.4 |
0.4 |
0.0 |
0.0 |
0.2 |
0.4 |
0.4 |
0.0 |
1.0 |
0.0 |
0.0 |
0.0 |
0.0 |
12 |
0.0 |
1.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.6 |
0.4 |
0.0 |
0.0 |
0.0 |
0.6 |
0.4 |
0.0 |
0.6 |
0.4 |
0.0 |
0.0 |
0.0 |
13 |
0.0 |
0.8 |
0.2 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.6 |
0.4 |
0.0 |
0.0 |
0.0 |
0.6 |
0.4 |
0.0 |
0.0 |
1.0 |
0.0 |
0.0 |
0.0 |
0.0 |
14 |
0.0 |
0.8 |
0.2 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.2 |
0.4 |
0.4 |
0.0 |
0.0 |
0.2 |
0.4 |
0.4 |
1.0 |
0.0 |
0.0 |
0.0 |
0.0 |
15 |
0.0 |
0.4 |
0.6 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.6 |
0.2 |
0.2 |
0.0 |
0.0 |
0.6 |
0.2 |
0.2 |
0.6 |
0.2 |
0.2 |
0.0 |
0.0 |
16 |
0.0 |
0.4 |
0.6 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.4 |
0.6 |
0.0 |
0.0 |
0.0 |
0.4 |
0.6 |
0.0 |
0.0 |
0.6 |
0.4 |
0.0 |
0.0 |
17 |
0.0 |
1.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.6 |
0.4 |
0.0 |
0.0 |
0.0 |
0.6 |
0.4 |
1.0 |
0.0 |
0.0 |
0.0 |
0.0 |
18 |
0.0 |
0.6 |
0.4 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.4 |
0.2 |
0.2 |
0.2 |
0.2 |
0.20000000000000007 |
0.2 |
0.2 |
0.2 |
0.4 |
0.6 |
0.0 |
0.0 |
0.0 |
19 |
0.0 |
0.8 |
0.2 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.6 |
0.2 |
0.2 |
0.0 |
0.2 |
0.4 |
0.2 |
0.2 |
0.0 |
0.6 |
0.4 |
0.0 |
0.0 |
0.0 |
DV_1-19.csv: reports decision variable estimates (repair cost, repair time, injuries) for each building asset.
DV |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Impractical |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Cost |
Repair Time |
Repair Time |
Repair Time |
Repair Time |
Repair Time |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
Injuries |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
comp_type |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
probability |
S |
S |
S |
S |
S |
S |
NS |
NS |
NS |
NS |
NS |
NSA |
NSA |
NSA |
NSA |
NSA |
NSD |
NSD |
NSD |
NSD |
NSD |
sev1 |
sev1 |
sev1 |
sev1 |
sev1 |
sev2 |
sev2 |
sev2 |
sev2 |
sev2 |
sev3 |
sev3 |
sev3 |
sev3 |
sev3 |
sev4 |
sev4 |
sev4 |
sev4 |
sev4 |
|||||
DSG_DS |
aggregate |
1_1 |
2_1 |
3_1 |
4_1 |
4_2 |
aggregate |
1_1 |
2_1 |
3_1 |
4_1 |
aggregate |
1_1 |
2_1 |
3_1 |
4_1 |
aggregate |
1_1 |
2_1 |
3_1 |
4_1 |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
aggregate |
||||||
stat |
mean |
std |
10% |
median |
90% |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
mean |
std |
10% |
median |
90% |
mean |
std |
10% |
median |
90% |
mean |
std |
10% |
median |
90% |
mean |
std |
10% |
median |
90% |
mean |
std |
10% |
median |
90% |
|
1 |
0.0766 |
0.098587220267132 |
0.005 |
0.027000000000000003 |
0.1916 |
0.0 |
0.0 |
0.0766 |
0.005 |
0.027000000000000003 |
0.08 |
0.266 |
0.0766 |
0.005 |
0.027000000000000003 |
0.08 |
0.266 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
|||||||||
2 |
0.06790000000000003 |
0.10501438591926347 |
0.0034500000000000004 |
0.027000000000000003 |
0.17692500000000005 |
0.0 |
0.00145 |
0.003625 |
0.06645000000000001 |
0.005 |
0.027000000000000003 |
0.27325 |
0.06500000000000003 |
0.005 |
0.027000000000000003 |
0.266 |
0.00145 |
0.007249999999999999 |
0.58 |
0.7103520254071216 |
0.0 |
0.0 |
1.45 |
0.000145 |
0.00017758800635178038 |
0.0 |
0.0 |
0.0003625 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
|||||||||
3 |
0.12327500000000002 |
0.12416358665083738 |
0.015975000000000003 |
0.030625000000000006 |
0.27542500000000003 |
0.0 |
0.002175 |
0.003625 |
0.1211 |
0.005 |
0.027000000000000003 |
0.27325 |
0.1182 |
0.005 |
0.027000000000000003 |
0.266 |
0.0029 |
0.007249999999999999 |
0.8699999999999999 |
0.7103520254071216 |
0.0 |
1.45 |
1.45 |
0.0002175 |
0.00017758800635178038 |
0.0 |
0.0003625 |
0.0003625 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
|||||||||
4 |
0.0911 |
0.10353626780022544 |
0.010075 |
0.030625000000000006 |
0.2177 |
0.0 |
0.0029 |
0.004833333333333333 |
0.0882 |
0.008625 |
0.027000000000000003 |
0.1235 |
0.27325 |
0.07660000000000003 |
0.005 |
0.027000000000000003 |
0.08 |
0.266 |
0.0116 |
0.007249999999999999 |
0.0435 |
1.16 |
1.085080642164443 |
0.0 |
1.45 |
2.3200000000000003 |
0.00029 |
0.00027127016054111073 |
0.0 |
0.0003625 |
0.00058 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
||||||
5 |
0.08865 |
0.09427295476434376 |
0.0079 |
0.08 |
0.1916 |
0.0 |
0.0 |
0.08865 |
0.008625 |
0.08 |
0.266 |
0.08720000000000001 |
0.005 |
0.08 |
0.266 |
0.00145 |
0.007249999999999999 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
||||||||||
6 |
0.036050000000000006 |
0.032783246483531814 |
0.0107 |
0.027000000000000003 |
0.07195000000000001 |
0.0 |
0.0029 |
0.004833333333333333 |
0.03315 |
0.01225 |
0.051166666666666666 |
0.0172 |
0.005 |
0.02700000000000001 |
0.01595 |
0.007249999999999999 |
0.0725 |
1.16 |
1.085080642164443 |
0.0 |
1.45 |
2.3200000000000003 |
0.00029 |
0.00027127016054111073 |
0.0 |
0.0003625 |
0.00058 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
||||||||||
7 |
0.050275 |
0.04010723126818904 |
0.010075 |
0.03425 |
0.09885 |
0.0 |
0.003625 |
0.006041666666666666 |
0.04665 |
0.008625 |
0.03425 |
0.090875 |
0.0394 |
0.005 |
0.027000000000000003 |
0.08 |
0.007249999999999999 |
0.0090625 |
1.45 |
1.2969194269498778 |
0.0 |
1.45 |
2.9 |
0.0003625 |
0.0003242298567374695 |
0.0 |
0.0003625 |
0.000725 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
|||||||||
8 |
0.10805 |
0.08188229356826786 |
0.048200000000000014 |
0.08 |
0.1945 |
0.0 |
0.0 |
0.10805 |
0.027000000000000003 |
0.08241666666666668 |
0.266 |
0.1066 |
0.027000000000000003 |
0.08 |
0.266 |
0.00145 |
0.007249999999999999 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
||||||||||
9 |
0.029125000000000005 |
0.01298075498574717 |
0.013800000000000005 |
0.03425 |
0.04005 |
0.0 |
0.000725 |
0.003625 |
0.0284 |
0.005 |
0.03425 |
0.0226 |
0.005 |
0.027000000000000003 |
0.0058 |
0.009666666666666664 |
0.29 |
0.5800000000000001 |
0.0 |
0.0 |
0.8700000000000001 |
7.25e-05 |
0.000145 |
0.0 |
0.0 |
0.00021750000000000006 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
|||||||||||
10 |
0.151325 |
0.12904455625868144 |
0.032075000000000006 |
0.08 |
0.3124 |
0.0 |
0.002175 |
0.0054375 |
0.14915 |
0.027000000000000003 |
0.08 |
0.305875 |
0.1332 |
0.027000000000000003 |
0.08 |
0.266 |
0.01595 |
0.007249999999999999 |
0.0725 |
0.8699999999999999 |
1.16 |
0.0 |
0.0 |
2.3200000000000003 |
0.0002175 |
0.00028999999999999995 |
0.0 |
0.0 |
0.00058 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
||||||||
11 |
0.0438 |
0.030629397643440526 |
0.013800000000000005 |
0.027000000000000003 |
0.08 |
0.0 |
0.0 |
0.0438 |
0.005 |
0.027000000000000003 |
0.08 |
0.0438 |
0.005 |
0.027000000000000003 |
0.08 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
|||||||||||
12 |
0.054000000000000006 |
0.028037474921968283 |
0.027000000000000003 |
0.0415 |
0.0887 |
0.0 |
0.0 |
0.054000000000000006 |
0.03183333333333333 |
0.08725 |
0.0482 |
0.02700000000000001 |
0.08 |
0.0058 |
0.0145 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
||||||||||||
13 |
0.014525 |
0.010271440989461995 |
0.005 |
0.008625 |
0.027000000000000003 |
0.0 |
0.000725 |
0.003625 |
0.013800000000000002 |
0.005 |
0.027000000000000003 |
0.013800000000000002 |
0.005 |
0.027000000000000003 |
0.0 |
0.29 |
0.58 |
0.0 |
0.0 |
0.8700000000000001 |
7.25e-05 |
0.000145 |
0.0 |
0.0 |
0.00021750000000000006 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
||||||||||||
14 |
0.144525 |
0.1011896857392096 |
0.048200000000000014 |
0.083625 |
0.266 |
0.0 |
0.000725 |
0.003625 |
0.1438 |
0.027000000000000003 |
0.08 |
0.266 |
0.1438 |
0.027000000000000003 |
0.08 |
0.266 |
0.0 |
0.29 |
0.5800000000000001 |
0.0 |
0.0 |
0.8700000000000001 |
7.25e-05 |
0.000145 |
0.0 |
0.0 |
0.00021750000000000006 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
||||||||||
15 |
0.09845 |
0.09682686223357648 |
0.028450000000000007 |
0.06687499999999999 |
0.20465000000000005 |
0.0 |
0.0029 |
0.004833333333333333 |
0.09555 |
0.03908333333333333 |
0.08 |
0.2805 |
0.0854 |
0.02700000000000001 |
0.08 |
0.266 |
0.01015 |
0.0145 |
0.03625 |
1.16 |
1.085080642164443 |
0.0 |
1.45 |
2.3200000000000003 |
0.00029 |
0.00027127016054111073 |
0.0 |
0.0003625 |
0.00058 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
||||||||
16 |
0.091425 |
0.04704609441813421 |
0.039325 |
0.0945 |
0.14525 |
0.0 |
0.003625 |
0.006041666666666666 |
0.08779999999999999 |
0.037875000000000006 |
0.12108333333333332 |
0.05880000000000001 |
0.027000000000000003 |
0.08 |
0.029000000000000005 |
0.009666666666666664 |
0.058 |
1.45 |
1.2969194269498778 |
0.0 |
1.45 |
2.9 |
0.0003625 |
0.0003242298567374695 |
0.0 |
0.0003625 |
0.000725 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
||||||||||
17 |
0.1544 |
0.09112101843153424 |
0.08 |
0.08 |
0.266 |
0.0 |
0.0 |
0.1544 |
0.08 |
0.266 |
0.1544 |
0.08 |
0.266 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
|||||||||||||
18 |
0.086475 |
0.0933870440692926 |
0.0165 |
0.045125 |
0.1945 |
0.0 |
0.002175 |
0.0054375 |
0.08430000000000001 |
0.017 |
0.0415 |
0.08 |
0.266 |
0.07560000000000001 |
0.005 |
0.027000000000000003 |
0.08 |
0.266 |
0.0087 |
0.0145 |
0.8699999999999999 |
1.16 |
0.0 |
0.0 |
2.3200000000000003 |
0.0002175 |
0.00028999999999999995 |
0.0 |
0.0 |
0.00058 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
|||||||
19 |
0.027750000000000004 |
0.02810827280357155 |
0.0059 |
0.01225 |
0.06170000000000001 |
0.0 |
0.00145 |
0.007249999999999999 |
0.0263 |
0.00816666666666667 |
0.027000000000000003 |
0.08 |
0.0234 |
0.005 |
0.027000000000000003 |
0.08 |
0.0029 |
0.007249999999999999 |
0.58 |
1.16 |
0.0 |
0.0 |
1.7400000000000002 |
0.000145 |
0.00029 |
0.0 |
0.0 |
0.0004350000000000001 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |