2.10. RV: Random Variables

The RV tab allows the user to specify the probabilistic distribution for the random problem at hand. The following probabilistic distributions for the random variables are currently supported:

2.10.1. Probability distribution

Note

To add a new random variable the user presses the Add button. To remove a random variable, the user must first select it by checking the small circle before the random variable, and then pressing the Remove button.

2.10.1.1. Dakota Engine

The following six distribution classes are supported for Dakota engine.

1. Normal (Gaussian)

   User provides the mean (\(\mu\)) and standard deviation (\(\sigma\)) of the normal distribution. The density function of the normal distribution, as a function of \(\mu\) and \(\sigma\) is:

   (2.10.1.1.1)\[f(x) = \frac{1}{\sqrt{2 \pi} \sigma} \exp \left( -{\frac{1}{2} \left( \frac{x - \mu}{\sigma} \right)^2} \right)\]

2. Lognormal

   User provides the mean (\(\mu\)) and standard deviation (\(\sigma\)) of the lognormal distribution. The density function of the lognormal distribution, as a function of \(\mu\) and \(\sigma\) is:

   (2.10.1.1.2)\[f(x) = \frac{1}{\sqrt{2 \pi} \zeta x} \exp \left( -{\frac{1}{2} \left( \frac{\ln x - \lambda}{\zeta} \right)^2} \right)\]

where \(\zeta^2 = \ln \left( \frac{\sigma^2}{\mu^2} + 1 \right)\) and \(\lambda = \ln(\mu) - \frac{\zeta^2}{2}\)

3. Beta

   User provides \(\alpha\), \(\beta\), lower bound (\(L_B\)), and an upper bound (\(U_B\)) for the beta distribution. The density function of the normal distribution, as a function of these quantities is:

   (2.10.1.1.3)\[f(x) = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)} \frac{(x - L_B)^{\alpha-1}(U_B-x)^{\beta-1}}{(U_B - L_B)^{\alpha + \beta - 1}}\]

   where \(\Gamma(\alpha)\) is the Gamma function.

4. Uniform

   User provides the lower bound (\(L_B\)), and an upper bound (\(U_B\)) for the uniform distribution. The density function of the normal distribution, as a function of these quantities is:

   (2.10.1.1.4)\[f(x) = \frac{1.0}{(U_B - L_B)}\]

   The mean of the distribution is \(\frac{(U_B + L_B)}{2.0}\)

5. Weibull

   User provides shape parameter (\(k\)) and scale parameter (\(\lambda\)) for the Weibull distribution. The density function of the Weibull distribution, as a function of these quantities is:

   (2.10.1.1.5)\[f(x) = \frac{k}{\lambda}\left(\frac{x}{\lambda}\right)^{k-1} \exp \left( -(x/\lambda)^{k} \right)\]

   where \(k,\lambda > 0\) and \(x \geq 0\). For \(x<0\), \(f(x) = 0\).

6. Gumbel

   User provides \(\alpha\) and \(\beta\) for the Gumbel distribution, where \(\beta\) is known as the location parameter and \(\frac{1}{\alpha}\) the scale parameter. The density function of the Gumbel distribution, as a function of these quantities is:

   (2.10.1.1.6)\[f(x) = \alpha e^{-\alpha(x-\beta)} \exp(-e^{-\alpha(x-\beta)})\]

For each random variable, the user must enter a name and select from the pull down menu the distribution associated with the random variable. For the distribution selected, the user must then provide the input arguments, which are as described above. Fig. 2.10.1.1.1 shows the panel for a problem with four Random Variables with all random input following Gaussian distributions.

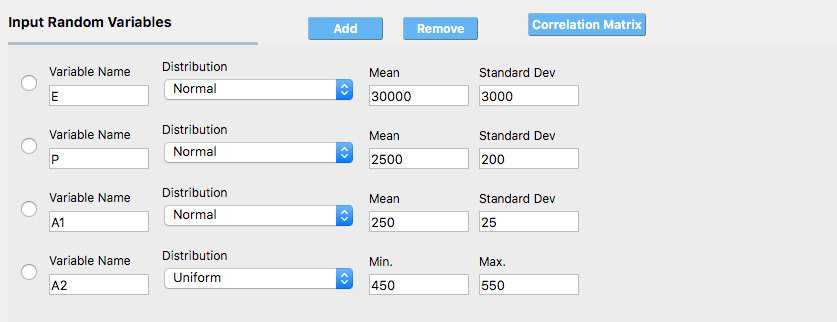
Fig. 2.10.1.1.1 Random variable specification.

Note

To add a new random variable the user presses the Add button. To remove a random variable, the user must first select it by checking the small circle before the random variable, and then pressing the Remove button.

Warning

Removing a random variable may have unintended consequences and cause the UQ engine to fail.

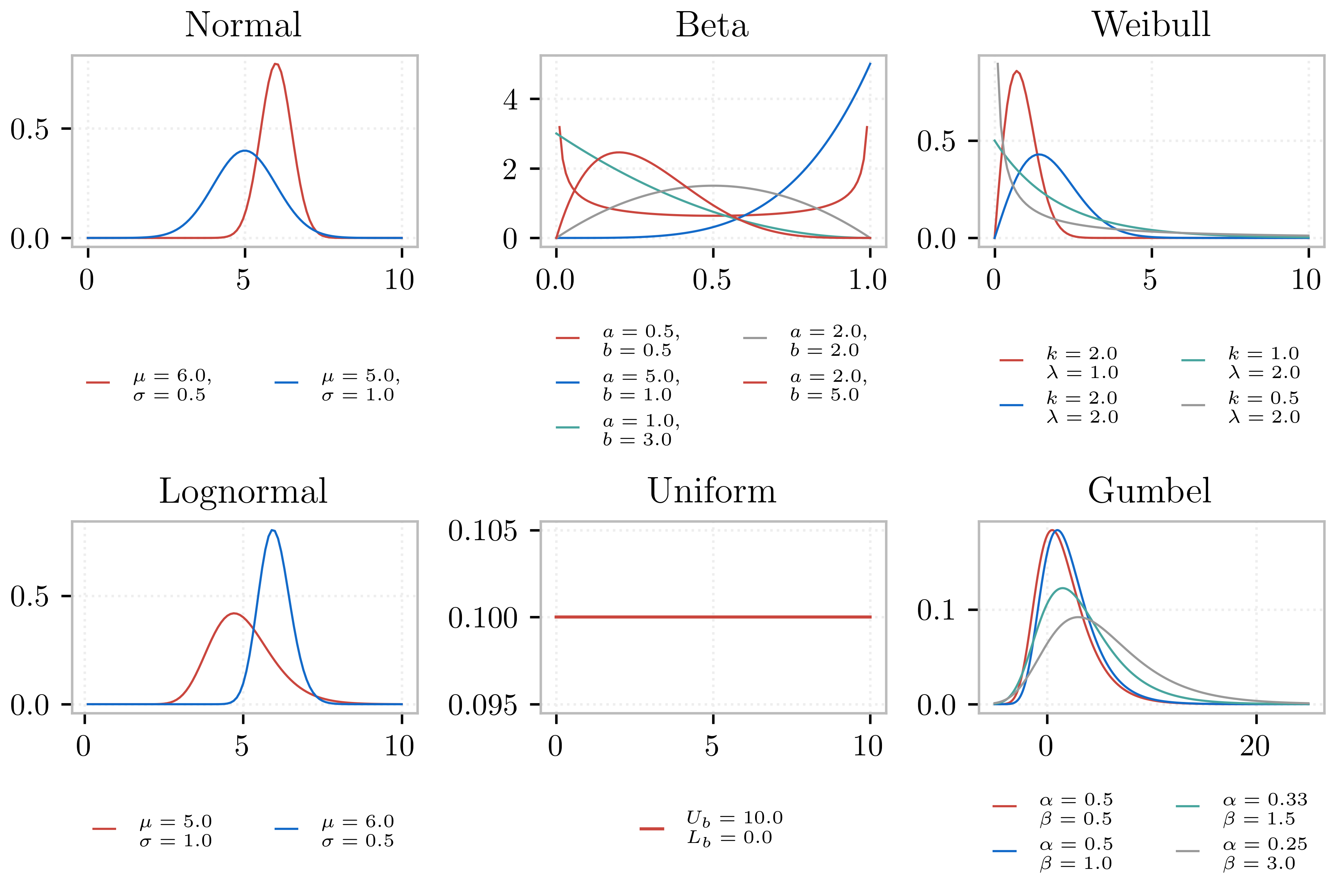
Fig. 2.10.1.1.2 Various distributions offered by the R2D app .